The Wave Equation
The Wave Equation |
|---|
|
The wave equation is a mathematical formula which has enormous universal application. Some people may claim that all physical process can be described by the wave equation. Many things do behave according to this equation and in our everyday experience we interact with numerous things which are waves, such as light, radio waves, micro-waves, radar, sound, vibration, water waves, thermal radiation, etc... For water waves, such as in the surf, the wave equation can be simplified and manipulated to show us some rather unusual relationships. All types of waves have some common features, such as the wave speed (how fast the wave moves), the amplitude of the wave, and the frequency or period of the wave. Note that for MOST waves, the speed of the wave is normally fairly constant and is independent of the wave frequency and amplitude. Water waves are somewhat peculiar in this respect and that is what makes them more interesting to study and of course be in. For water waves, the speed of the wave is very dependent on the water depth AND the frequency. After much math and manipulation, the wave equation can be reduced to some simpler relationships which help to show this. The wave equation starts as the deceivingly simple formula which is the logo of the The Wave Equation product line. This very simple form of the wave equation is attributed to d'Alembert who did much to help solve the wave equation. D'Alembert was a young, brilliant, and rather tragically interesting mathematician who died at a very young age in a dual instigated by a love triangle. He was also a passionate participant in the French revolution and an orphan. If one solves the wave equation for the wave velocity of a water wave one gets: where, If you look at this equation you see something interesting - The wave velocity depends on the wavelength of the wave and the depth of the water. There is also this confusing thing "tanh" which will look strange to most people. To help simplify this a bit more, there are two special cases of waves which occur frequently: waves tend to be either "deep" water waves, or "shallow" water waves. Deep water waves are waves that have a wavelength which is much smaller than the depth of the water. Shallow water waves are waves with wavelengths that are much larger than the depth of the water. Surfers are normally in shallow water waves. A deep water wave has a wavelength which is less than twice the depth of the water. If you were in 10 feet of water, a deep water wave would have a wave length of 5 feet or less. A wavelength of 5 feet or less is chop. A shallow water wave has a wavelength that is greater than 20 times the depth. Once again, you are in 10 feet of water, a shallow water wave has a wavelength greater than 200 feet. That is more like the waves one tries to catch. This thing called "tanh" is called the hyperbolic tangent function. This is somewhat similar to the tangent function taught in high school trig, but whereas the standard tangent function is related to circles, the hyperbolic tangent is (surprise) related to hyperbolas. Hyperbolas and circles are actually related to each other along with ellipses and parabolas in what are called conic sections. Suffice to say that the hyperbolic tangent is like the regular tangent but for hyperbolas instead of circles. Strangely enough, hyperbolic functions are fairly common in describing how the world works. For our purposes, as the argument of the tanh becomes large, the value approaches 1.0. As the argument of the tanh becomes small, the value approaches the argument. For deep water waves the argument is large and one gets for the velocity: For shallow water waves, the argument is small and one gets for the velocity, Looking at shallow water waves, one sees that as the water depth becomes small, the velocity drops. So when the depth of the water is zero, the velocity is zero. So as a wave moves towards the shore into water depths that are decreasing in depth, the wave slows down. Another parameter of interest now if the wave period. This is the time between waves. Essentially the wave period remains constant, but as the wave approaches the shore, the depth drops and the speed slows down. If the period remains constant, then the only way for the speed to slow down is for the wavelength to also decrease. This groups waves together into what we sometimes call sets. Of course a "set" is a subjective description of a preferable group of larger waves. The creation of larger local wave swells occurs further out in the ocean where waves of varying frequencies merge together and either reinforce each other to make larger waves or interfere with each other and make smaller or no waves. |

Copyright (c) 2006 Ventura Enterprises. All rights reserved.






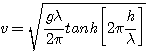
 - wave velocity
- wave velocity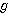 - acceleration due to gravity
- acceleration due to gravity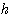 - depth of the water
- depth of the water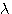 - wavelength of the wave
- wavelength of the wave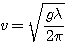 .
. 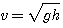 .
.